Fourier Series, An Example
Table of Contents
Plot de uma série de Fourier
Função à descrever
\begin{equation}
\begin{aligned}
f(x) =
\begin{cases}
1, \quad 0\leq\text{x}<\pi\\
0, \quad -\pi\leq\text{x}<0\\
\end{cases}\\
\text{periodic with period T}=2\pi
\end{aligned}
\end{equation}
Solução analítica
Usando,
Chegamos em,
O que significa que
Implementação em Julia
A função aproximação da série de Fourier
function f(x,N)
g = 1/2
for k in 1:1:N
g += (2/((2*k -1)*π))*sin((2*k-1)*x)
end
return g
end
Mapeamos os valores para o intervalo que queremos estimar a função periódica
values = map(x -> f.(-4*π:0.01:4*π,x), 1:1:100)
Por fim, definimos a função real, a qual queremos aproximar
function f_actual(x)
if abs(x)<π
if 0<=x<π
return 1
elseif -π<=x<0
return 0
end
else
y = (x/2π -floor(x/2π))*2π
if π<=y<2π
return 0
elseif 0<=y<π
return 1
end
end
end
Gerando os valores literais
values_actual = f_actual.(-4*π:0.01:4*π)
Plot
Usaremos a biblioteca PlotlyJS.jl, para gerarmos um gráfico de alta qualidade,
trace = PlotlyJS.scatter(;x=xs, y=values[10])
trace2 = PlotlyJS.scatter(;x=xs, y=values[100])
trace3 = PlotlyJS.scatter(;x=xs, y=values_actual)
PlotlyJS.plot([trace,trace3])
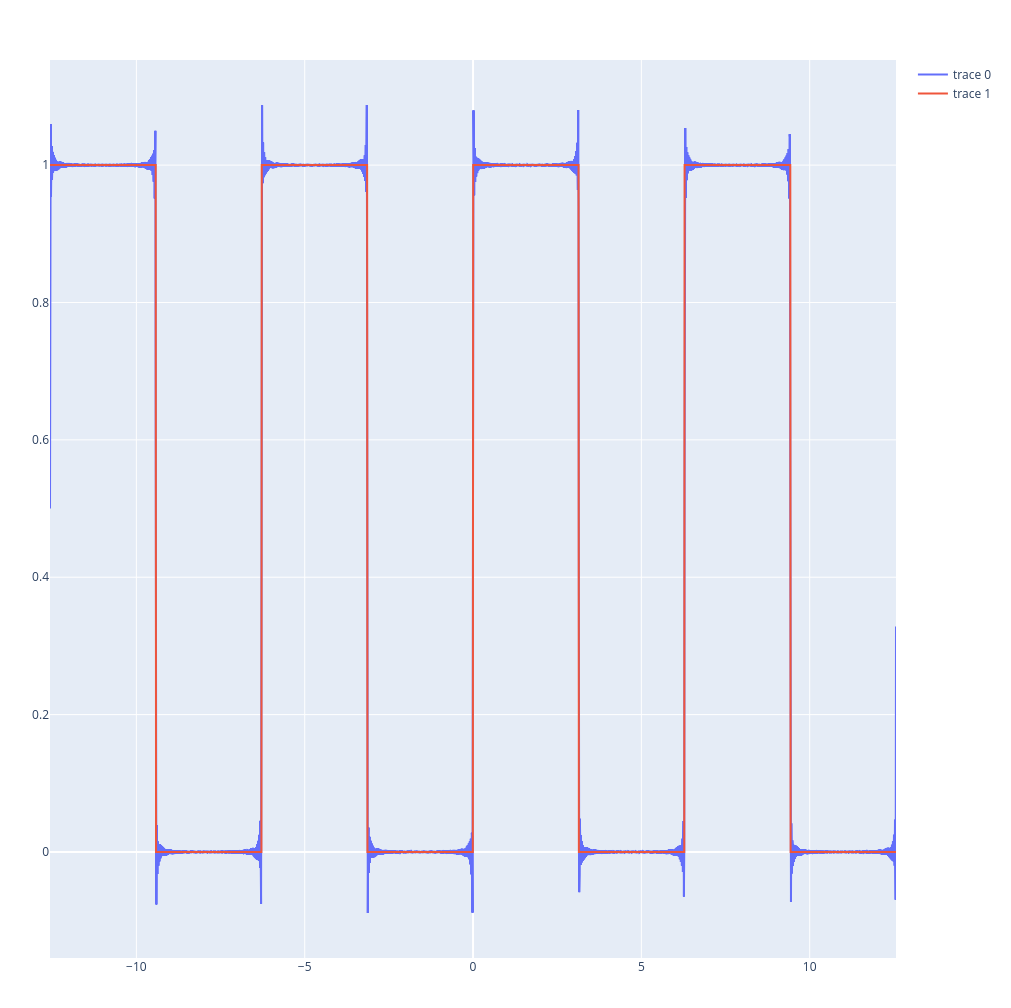
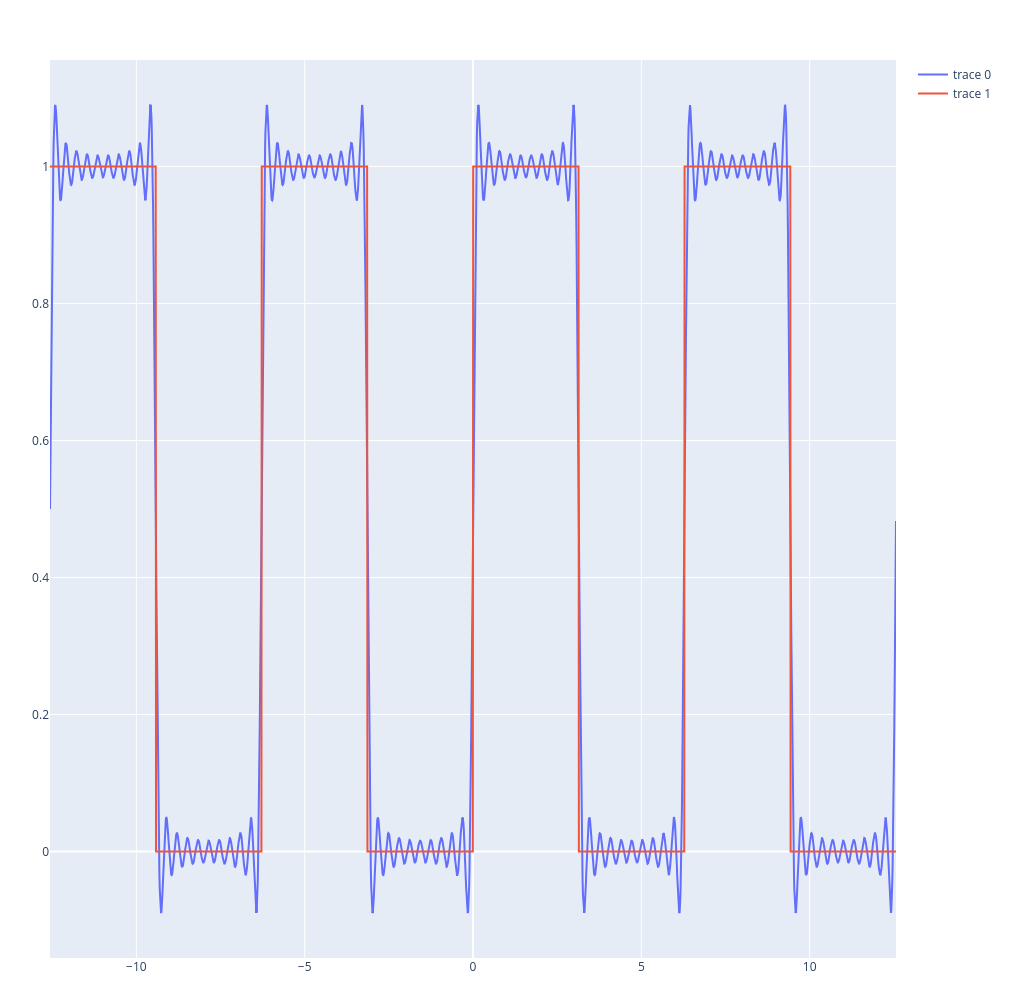
Fourier com 10 termos de aproximação
PlotlyJS.plot([trace2,trace3])
Fourier com 100 termos de aproximação
