Noise-Signal ratios (F-tests) - (SS)
How to classify Groups scientifically (F-tests)
Let's imagine we have four normaly-distributed groups with different 'intrinsic' variability in regards to belief on a given subject.
Can we group them without lossing generality? Is the error commited too great in this categorization? Let's find out!
We can use scipy, numpy and matplotlib to help us through our thoughts
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
Visualizing these many distributions
#x-axis
x = np.arange(20, 95, 0.001)
## background
plt.figure(facecolor='#FFF0F5')
###define normal values (not normalized)
plt.plot(x, norm.pdf(x, 50, 12), label='μ: 50, σ: 12', color='k')
plt.plot(x, norm.pdf(x, 49.7, 6), label='μ: 49.7, σ: 6', color='violet')
plt.plot(x, norm.pdf(x, 53, 3), label='μ: 53, σ: 3', color='blue')
plt.plot(x, norm.pdf(x, 51.3, 17), label='μ: 51.3, σ: 17', color='red')
# Axis titles
plt.xlabel('Degree of belief in a subject X')
plt.ylabel('Probability')
#add legend to plot
plt.legend()
plt.show()
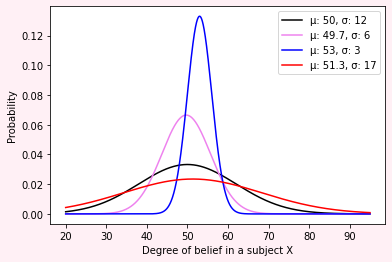
Ok, we see these are all close to one another. At the same time, some groups are more orthodox, as blue, which has extremely narrow possible views about this subject X.
So, the question is, can we categorize them as one thing (holding the same belief), without committing overgeneralization?
The Hypothesis
S1: Hypothesis undirectional ANOVA
Can we measure the behavior of these four groups as the same, without loss of generality?
The Null and Alternative Hypothesis follow,
That is, either they can or can not be treated as the same.
The Analysis Of Variance (ANOVA) method is perfectly suited for that
We will have a more in-depth knowledge of the origins and the mathematical basis of ANOVA's in other posts.
Let's dive in solving our mystery first. Just an overview:
- ANOVA will compare differences of means using standard variations
- There are the Within measures of groups.
- There are the Between measures of groups.
- Generally, if we wanted to compare directly among two groups, we would use:
- T-tests
- Z-tests
Why use it instead of T-tests and Z-tests
By using the Variations as our way of comparison, we can abstract the fact we are dealing with n-groups and concentrate in a one-dimensional variable.
If we were to deal with means to derive these conclusions, we couldn't take that approach. We rather would have to make six T-tests:
What does it measure, exactly?
Our final measure we'll be look at is the F-ratio:
- The Variation inside groups can be estimated by
- The Variation among different groups can be estimated by
But, the Between estimator also takes the Within variation as a baseline. So, truly, it can be seen as
Thus, F is a ratio to measure how much of
- The Variation inside groups can be estimated by
Finally, computation
Now that we had an overview of what we need to compute an ANOVA and how it work, let's do the Math.
A priori threshold for certainty
In Statistics, we can choose levels of causality and certainties we are prepared to accept as truth. Here, we will adopt the
Degrees of freedom
An abstract concept we use to compute are degrees of freedom. In this case we have 4 groups and - let's arbitrarily say we took 4 people and measured them in each group. So,
Our cutoff
Looking at a table,
This is our cutoff.
Variations and F
Generally, we have,
- n: quantity of people measured per group
- N: quantity of groups
- GM: mean of means
Thus,
Finally,
.
Comparison with a table and cutoff
As
In this case, we could say all these four groups could be treated as the same (average-wise).
Do you agree? Well, either you do or not, that's scientific scrutiny, right there. In a research that would be the conclusions we would arrive at!
If you want to learn more, check out the other Statistical Series (SS) posts in the website